Katharine Hunt

Research
Quantum Theory
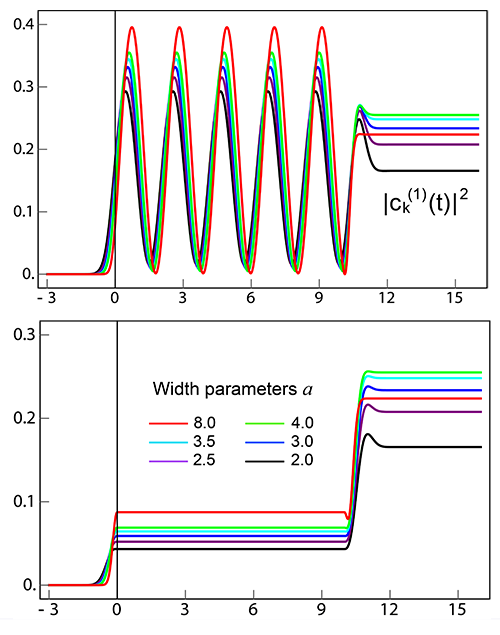
Quantum systems in time-dependent fields — We have derived new theoretical results for transition probabilities in quantum systems in timedependent electromagnetic fields. These results challenge Dirac’s expression for the transition probability, which depends on the norm-square of the coefficient ck(t) for the excited state | k0 〉 of the original unperturbed Hamiltonian H0, in the time-dependent wave function. By integrating by parts, Landau and Lifshitz separated ck(t) into an adiabatic term ak(t) that follows the adiabatic theorem of Born and Fock, and a nonadiabatic term bk(t) that depends on the time-derivative of the perturbation up to time t. The adiabatic term describes the adjustment of the initial state to the perturbation without actual transitions, while the transition probability is given by the norm-square of bk(t). Our work reinforces this statement and goes beyond the results of Landau and Lifshitz. We proved that the energy separates into adiabatic and nonadiabatic terms. The nonadiabatic term in the energy is given by the sum over excited states of | bk(t) |2 times the transition energy (Ek – E0), corrected for the perturbation. We proved that the power absorbed by a molecule from an electromagnetic field is equal to the time-derivative of the nonadiabatic term in the energy. Further, the vibrational wave packets associated with ak(t) and bk(t) evolve on different electronic potential energy surfaces. Our results for transition probabilities differ significantly from the results of Dirac’s theory, during short perturbing pulses with frequencies that are off-resonant from the transition frequency. For a cosine wave of frequency ω in a Gaussian envelope, | bk(t) |2 is larger than | ck(t) |2 when ω > ωk0, the transition frequency to state k; while the opposite is true when ω < ωk0. These results are independent of the phase of the oscillating wave relative to the peak of the Gaussian envelope. The differences are also quite stark for a perturbing pulse that rises to a level plateau, and later falls off. While the perturbation is constant, the nonadiabatic transition probability is constant as required physically, since a static perturbation cannot induce transitions; in contrast Dirac’s form of the transition probability continues to oscillate while the perturbation is constant, as shown in Figure 1.
Collision-induced spectroscopic processes - Spectroscopic processes that are forbidden for single molecules are observed in dense gases and liquids, because the electronic charge distorts during molecular collisions. Our work has focused on collision-induced absorption in the IR by H2 gas, H2/H and H2/He mixtures, N2 gas and O2 gas, with applications in astrophysics and in atmospheric profiling. Interaction-induced absorption affects the radiative profiles of gases in star-forming nebulae; very old, very cool white dwarf stars; the outer planets and exoplanets that are termed “hot Jupiters” and “warm Neptunes,” and the atmospheres of satellites of the outer planets. My research group calculates the total dipole moments ab initio and then expresses the results in spherical-tensor form for subsequent line-shape calculations. Dipole surfaces for H2-H are shown in Figure 2. This research area involves collaborations with Lothar Frommhold and Martin Abel (University of Texas, Austin), Magnus Gustafsson (Luleå, Sweden), Tijs Karman, Gerrit Groenenboom, and Ad van der Avoird (Nijmegen, the Netherlands), and Richard Dawes (Missouri University of Science and Technology).
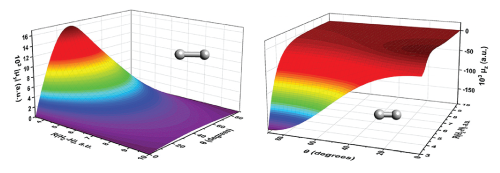
components of the
dipole of H2-H, figures
from AIP Scilight 2019,
220002-1 by Adam
Liebendorfer, a report
of work by H.-K. Lee, X.
Li, E. Miliordos, and K. L.
C. Hunt, J. Chem. Phys.
2019, 150, 204307.
Contact / Webpage
Area(s) of Interest
Theoretical and Computational (Th)
Biological (Bi)
Chemical Physics (CP)
Material (Ma)
Physical (Ph)
Selected Publications
Variance of the energy of a quantum system in a time-dependent perturbation: Determination by nonadiabatic transition probabilities, A. Mandal and K.L.C. Hunt, J. Chem. Phys. 2020, 152, 104100.
The interaction-induced dipole of H2-H: New ab initio results and spherical tensor analysis, Hua-Kuang Lee, Xiaoping Li, Evangelos Miliordos, and Katharine L. C. Hunt, J. Chem. Phys. 2019, 150, 204307, Featured Article.
Dependence of the multipole moments, static polarizabilities, and static hyperpolarizabilities of the hydrogen molecule on the H-H separation in the ground singlet state, Evangelos Miliordos and Katharine L. C. Hunt, J. Chem. Phys. 2018, 149, 234103.
Nonadiabatic transition probabilities in a time-dependent Gaussian pulse or plateau pulse: Toward experimental tests of the differences from Dirac’s transition probabilities, Anirban Mandal and Katharine L. C. Hunt, J. Chem. Phys. 2018, 149, 204110, Editor’s Pick.
Quantum transition probabilities during a perturbing pulse: Differences between the nonadiabatic results and Fermi’s golden rule forms, A. Mandal and K. L. C. Hunt, J. Chem. Phys. 2018, 148, 194107.
Gauge-invariant expectation values of the energy of a molecule in an electromagnetic field, Anirban Mandal and Katharine L. C. Hunt, J. Chem. Phys. 2016, 144, 044109.
Non-adiabatic current densities, transitions, and power absorbed by a molecule in a time-dependent electromagnetic field, Anirban Mandal and Katharine L. C. Hunt, J. Chem. Phys. 2015, 143, 034102.
Quantum mechanical calculation of the collision-induced absorption spectra of N2-N2 with anisotropic interactions, Tijs Karman, Evangelos Miliordos, Katharine L. C. Hunt, Gerrit C. Groenenboom, and Ad van der Avoird, J. Chem. Phys. 2015, 142, 084306.
Adiabatic and nonadiabatic contributions to the energy of a system subject to a timedependent perturbation, Anirban Mandal and Katharine L. C. Hunt, J. Chem. Phys. 2012, 137, 164109.
Awards/Honors
| Year | Award | Organization |
|---|---|---|
| 2020 | Norman L and Olga K. Fritz Excellence in Teaching Award | College of Natural Science |
| 2009 | Distinguished Career Prize | International Conference of Computational Methods in Science and Engineering |
| 2001 | Senior Faculty Award | Sigma Xi Honor Society (Michigan State University) |
| 1998 - 2002 | Member | Midwest Chemistry Chairs’ Group |
| 1998 - 2003 | Selection Committee Member (appointed by British Consul General) | Marshall Scholarship Program, Midwest Region |
| 1998 | Outstanding Mentor Award | Ronald McNair Summer Undergraduate Research Opportunities Program |
| 1998 - 2002 | Chairperson | Michigan State University (Department of Chemistry) |
| 1995 - 1997 | Councilor for Physical Chemistry | American Chemical Society |
| 1992 - 2022 | University Distinguished Professor | Michigan State University |
| 1991 | Junior Faculty Award | Sigma Xi Honor Society (Michigan State University) |
| 1978 - 1979 | NSF National Needs Postdoctoral Fellowship | National Science Foundation |
| 1975 - 1978 | Danforth Fellowship | |
| 1975 | Phi Beta Kappa | |
| 1975-1975 | Danforth Fellowship | |
| 1975 - 1978 | Marshall Scholarship | United Kingdom |